Answer:
The point of maximum growth is at x=0.82
Explanation:
Given a logistic function
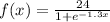
we have to find the point of maximum growth rate for the logistic function f(x).
From the graph we can see that the carrying capacity or the maximum value of logistic function f(x) is 24 and the point of maximum growth is at
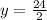 i.e between 0 to 12
i.e between 0 to 12
So, we can take
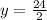 and then solve for x.
and then solve for x.
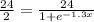
⇒
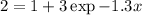
⇒
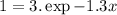 ⇒
⇒
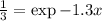
⇒ log 3=-1.3x
⇒ -0.4771=-1.3.x ⇒ x=0.82
Hence, the point of maximum growth is at x=0.82