Answer:
1) Known information:
- The perimeter.
-
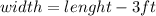
- The formula of the perimeter of the rectangle:
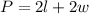
Unknown information:
- The value of the widht.
- The value of the length.
2) Equation:
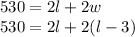
3)
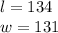
Explanation:
1. The problem gives you the perimeter, the formula of the perimeter of a rectangle and says that the width of a rectangle is 3 feet shorter than its length (
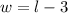 ), but does not give the value of the widht and the value of the lenght.
), but does not give the value of the widht and the value of the lenght.
2. Based on the information given, you can write the following equation:

Where
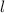 is the lenght and
is the lenght and
 is the width.
is the width.
Substitute
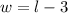 into the equation above, then you have:
into the equation above, then you have:
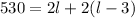
3. Solve for the lenght:
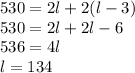
4. Know you can calculate the width:
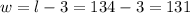
5. Therefore, the length is 134 feet and the widht is 131 feet.