Answer:
-2/3
Explanation:
We are to find the slope of a line which is perpendicular of a line with an equation
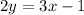 .
.
We know that the slope of line which is perpendicular to another line is the negative reciprocal of that perpendicular line.
So writing the given equation of a line in the slope intercept form:
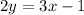 --->
--->
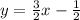
Here the slope of this line is
 so the slope of a line which is perpendicular to the given line will be
so the slope of a line which is perpendicular to the given line will be
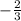 .
.