Question

What is the answer ?

Answer 1

Thus, option (c) is correct.

β = 61.5

Explanation:

Given ,
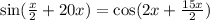`\sin ((x)/(2)+20x)=\cos(2x+(15x)/(2))` , we have to solve for x, and then find the value of β ( β > α )

Consider
`\sin ((x)/(2)+20x)=\cos(2x+(15x)/(2))`,

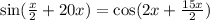First solve for x ,

`\Rightarrow \sin ((x)/(2)+20x)=\cos(2x+(15x)/(2))`

`\Rightarrow \sin ((x+40x)/(2))=\cos((4x+15x)/(2))`

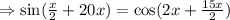
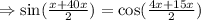
Thus,
`\Rightarrow \sin ((41x)/(2))=\cos((19x)/(2))`

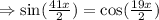
Also,
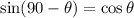`\sin (90-\theta)=\cos \theta` , we get,

Thus,
`\Rightarrow \cos (90-(41x)/(2))=\cos((19x)/(2))`

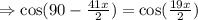
since, LHS = RHS thus, angle must be equal,

`\Rightarrow 90-(41x)/(2)=(19x)/(2)`

`\Rightarrow 90=(19x)/(2)+(41x)/(2)`

`\Rightarrow 90=(19x+41x)/(2)`

`\Rightarrow 90=(60x)/(2)`

`\Rightarrow x=3`

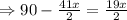
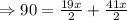
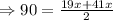
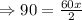
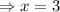
Thus,
`(x)/(2)+20x=(3)/(2)+20(3)=(3)/(2)+60=61.5` ,

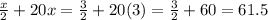Other angle can be found using angle sum property, as sum of angle of a triangle is 180°

Let third angle be y, then ,

90 + 61.5 + y = 180°

y = 180° - 151.5°

y = 28.5°

Since ( β > α ) ⇒ β= 61.5 and α = 28.5

Thus, option (c) is correct.

⇒ β = 61.5