Question

Which graph represents a piecewise function ?

Answer 1

Option A.

Explanation:

The given piecewise function is

`y=\begin{cases}x+3 & \text{ if } x<0 \\2x & \text{ if } x\geq 0\end{cases}`

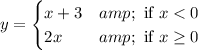
We need to find the graph of given function.

For
`x<0, f(x)=x+3`, so the table of values is

x y

-1 2

-2 1

-3 0

Because x<0, so for this piece of function there is an open circle at x=0.

For
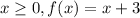`x\geq 0, f(x)=x+3`, so the table of values is

x y

0 0

1 2

2 4

Because
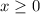`x\geq 0`, so for this piece of function there is a close circle at x=0, i.e., (0,0).

Only graph A passes through the points, which are mentioned in the above tables.

Therefore, the correct option is A.

Answer 2

A

Explanation:

A does. There is a gap at zero. A and D are your only real choices. Both show what happens at zero with minor variations and the devil is in the details. D shows that x is open ended when x = 0. That is not correct. The value should be x≥0 so y=2x is closed at x=0.

D is incorrect.

The answer is A.