Question

Dotti and Bud bought two identical watermelons. Dotti cut her watermelon into 3 pieces and ate 2 of the pieces. Dud cut his watermelon into 9 pieces, but ate the exact same amount of watermelon as Dotti. How many of 9 pieces must he have eaten of hes watermelon? Explain your answer.

Answer 1

Bus must have eaten 6 pieces of his watermelon.

Explanation:

We have been given that Dotti and Bud bought two identical watermelons. Dotti cut her watermelon into 3 pieces and ate 2 of the pieces. This means Dotti has eaten 2/3 of his watermelon.

Bud cut his watermelon into 9 pieces, but ate the exact same amount of watermelon as Dotti.

We will use proportions to solve our given problem as proportions states that two fractions are equivalent.

`\frac{\text{Pieces of watermelon eaten by Bud}}{\text{Total pieces of Bud's watermelon}}=\frac{\text{Pieces of watermelon eaten by Dotti}}{\text{Total pieces of Dotti's watermelon}}`

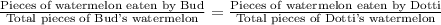
Upon substituting our given values in above proportion we will get,

`\frac{\text{Pieces of watermelon eaten by Bud}}{9}=(2)/(3)`

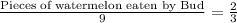
Let us multiply both sides of our equation by 9.

`\frac{\text{Pieces of watermelon eaten by Bud}}{9}*9=(2)/(3)*9`

`\text{Pieces of watermelon eaten by Bud}=2*3`

`\text{Pieces of watermelon eaten by Bud}=6`

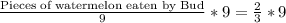
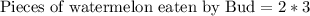
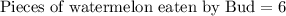
Therefore, Bud must have eaten 6 pieces of his watermelon.

Let us cross check our answer by substituting 6 in our proportion as:

`(6)/(9)=(2)/(3)`

`(2)/(3)=(2)/(3)`

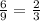
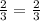
Hence, proved.

Answer 2

Bud have eaten 2 pieces as Bud and Dotti have eaten exact same amount.

Explanation:

We have been given Dotti and Bud bought two identical watermelons

Dotti cut her watermelon into 3 pieces and ate 2 of the pieces.

Bud cut watermelon into 9 pieces

But Dotti and Bud have eaten exact same amount of watermelon

That means if Dotti have eaten 2 pieces then Bud would also have eaten 2 pieces out of 9.