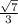Question

Find the exact value of cot Ø if csc Ø = -4/3 and and the terminal side of Ø lies in Quadrant III

Answer 1

√7/3.

Explanation:

csc Ø = 1 / sin Ø = 1 / -4/3 = -3/4.

As the sine is the opposite / hypotenuse the side adjacent to angle Ø will have length √(4^2 - 3^2) = √7 (by the Pythagoras theorem) and as the angle is in the third quadrant this will be -√7.

So cot Ø = adjacent / opposite = -√7/ -3

= √7/3 (answer).

Answer 2

`cot \theta= (√(7) )/(3)`

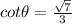
Explanation:

It is given that cosec
`\theta`=-4/3 and sin theta =1/cosec theta

so sin theta =-3/4 now since sin theta is perpendicular/hypotenuse, the third side base will be
`\sqrt({4}^(2)- (-3)^(2))\\  =√(16-9)\\ =√(7)`

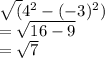
and we know that cot theta is inverse of tan so it will be base/perpendicular

i.e
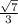`(√(7) )/(3)` and also it is given that side of theta is in quadrant III so cot theta will be positive, so final answer will be

`(√(7) )/(3)`