Question

Find the volume V of the solid obtained by rotating the region bounded by the given curves about the specified line. y = ln(3x), y = 1, y = 5, x = 0; about the y-axis

Answer 1

The volume of the solid formed by rotating the region bounded by the given curves about the y-axis is calculated using the cylindrical shells method, solving for x in terms of y and then computing the resulting integral from y=1 to y=5.

To find the volume of the solid obtained by rotating the region bounded by the curves ln y=ln(3x), y=1, y=5, and x=0 about the y-axis, use the method of cylindrical shells. Follow these steps: Determine the bounds of integration by finding the x-values where the curves intersect.

To find the intersection points: y=ln(3x) and y=1 ln(3x)=1 3x=
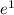`e^1` x=e/3 The bounds of integration are x=0 to x=e/3

​Set up the integral formula for the volume using cylindrical shells:

The outer radius is the distance from the y-axis to the curve y=5, which is 5−0=5. The inner radius is the distance from the y-axis to the curve Write the integral with the given bounds:

Write the integral with the given bounds:

V=2π∫ᵉ/³₀ x⋅(5−ln(3x))dxy=ln(3x)dx

Evaluate the integral using the bounds from x=0 to x=e/3 Calculate the definite integral to find the volume of the solid generated by rotation about the y-axis using the cylindrical shells method.

Answer 2

Using the disk method, the volume is obtained with the integral

`\displaystyle\pi\int_(y=1)^(y=5)\left(\frac{e^y}3\right)^2\,\mathrm dy=\frac\pi9\int_1^5e^(2y)\,\mathrm dy`

The radius of each disk is given by the horizontal distance from the axis of revolution,
`x=0`, to the logarithmic curve which we can write as a
`x(y)`:

`y=\ln(3x)\implies e^y=e^(\ln3x)=3x\implies x=\frac{e^y}3`

Then the volume of one such disk is
`\pi x(y)^2`.

The volume of the entire solid would be

`\displaystyle\frac\pi9\int_1^5e^(2y)\,\mathrm dy=\frac\pi{18}\int_1^52e^(2y)\,\mathrm dy=\frac\pi{18}\int_1^5e^(2y)\,\mathrm d(2y)`

`=\frac\pi{18}\left(e^(10)-e^2\right)`