Question

The combined average weight of an okapi and a llama is 450450 kilograms. The average weight of 33 llamas is 190190 kilograms more than the average weight of one okapi. On average, how much does an okapi weigh, and how much does a llama weigh?

Answer 1

Okapi 290 kg

Llama 160 kg

Explanation:

Let weight of each llama be
`l`

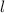
Let weight of each okapi be
`o`

Given, combined weight of 1 okapi and 1 llama is 450, we can write:

`l+o=450`

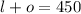
Also, average weight of 3 llama is 190 more than the average weight of 1 okapi, thus we can write:

`3l-190=o`

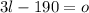
Now, substituting 2nd equation into 1st equation, we can solve for weight of 1 llama:

`l+o=450\\l+(3l-190)=450\\l+3l-190=450\\4l=450+190\\4l=640\\l=(640)/(4)=160`

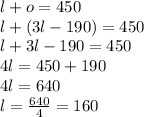
Each llama weights 160 kg, now using this and plugging into 2nd equation, we get weight of 1 okapi to be:

`o=3l-190\\o=3(160)-190\\o=290`

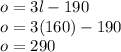
Each okapi weigh 290 kg