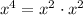 . Multiplying the denominator by
. Multiplying the denominator by
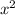 gives
gives
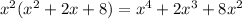
Subtracting this from the numerator gives a remainder of
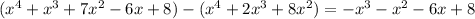
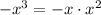 . Multiplying the denominator by
. Multiplying the denominator by
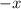 gives
gives
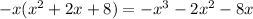
and subtracting this from the previous remainder gives a new remainder of
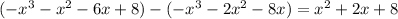
This last remainder is exactly the same as the denominator, so
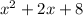 divides through it exactly and leaves us with 1.
divides through it exactly and leaves us with 1.
What we showed here is that
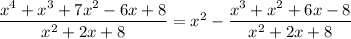
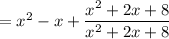
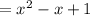
and this last expression is the quotient.
To verify this solution, we can simply multiply this by the original denominator:
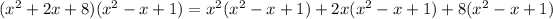
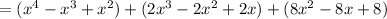
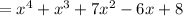
which matches the original numerator.