Question

A campus survey of OWLs indicates that 7% are charming, 4% are modest, and 3% are both charming and modest. Find the probability that an OWL is modest, given that he/she is charming. Given that a student isn't modest, what is the probability that they are not charming?

Answer 1

P(modest | charming) = 0.4286

P(not charming | not modest) = 0.896

Explanation:

This is a conditional probability problem.

Let A and B be two dependent events, then:

The probability of A given B is written as:

P (A | B) =
`(P(A\ and\ B))/(P(B))`

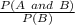
So:

The probability that an OWL is modest given that he/she is charming is:

P (modest | charming) =
`\frac{P(modest\ and\ charming)} {P(charming)}`

P (modest | charming) =
`(0.03)/(0.07)`

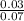
P (modest | charming) = 0.4286

Then, the probability that a student is not modest is:

`1- P(modest) = 1 - 0.04 = 0.96`

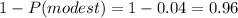
The probability that a student is not charming and not modest is:

`1- [P(charming\ or\ modest)]\\\\ = 1-[0.07 + 0.04 - 0.03]= 0.92`

So:

P(not charming | not modest) =
`(P(not\ charming\ and\ not\ modest))/(P(not\ modest))`

P(not charming | not modest) =
`(0.92)/(0.96)`

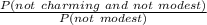
P(not charming | not modest) = 0.9583