Question

What are the explicit equation and domain for a geometric sequence with a first term of 4 and a second term of −8?

an = 4(−2)n − 1; all integers where n ≥ 0
an = 4(−2)n − 1; all integers where n ≥ 1
an = 4(−12)n − 1; all integers where n ≥ 1
an = 4(−12)n − 1; all integers where n ≥ 0

Answer 1

Pretty sure it's B.

Explanation:

The first person offered a pretty good explination and I'm taking the test.

Answer 2

Option B is right

Explanation:

Given:

There is a geometric sequence with first term =4

and second term =-8

We know that a geometric sequence is a sequence of numbers, in which each successive number is got by multiplying the previous number by a fixed value called common ratio.

First term is called a.

and common ratio is denoted by r.

The terms would be

`a,ar,ar^(2) ,...`

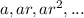
Here we have a=4 and ar =-8

So r =common ratio =-2

nth term we mean n can take values as 1,2.....

So general term

`a_(n)=ar^(n-1)\\  =4(-2)^(n-1),n\geq1`

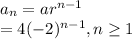
is right answer

Hence option b.