Answer:
Point of intersection (4,5)
Explanation:
5x + 3y - 35 = 0
3x - 4y = -8
⇒ 5x + 3y = 35
3x - 4y = -8
Matrix A will be formed by the coefficient of x and y. Matrix B will be formed by the constants.
![\sf A = \left[\begin{array}{cc}5&3\\3&-4\end{array}\right]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/wyurv4qvkqi6fjku3jaa.png)
![\sf B = \left[\begin{array}{c}35&-8\end{array}\right]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/qmdndrzcrgsu2uk8dkgh.png)
AX = B
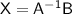
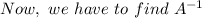 ,
,
Find the workout in the document attached.