Question

What is the common difference d of the sequence?

-15, -4, 7, 18, 29, ...

Question 1 options:

11


-11


12


-12

Question 2 (1 point)
What is the 8th term in the sequence?

an=25−3n
Question 2 options:

1


59


-6


22

Question 3 (1 point)
Which answer is the explicit rule for the sequence:

15.5, 13, 10.5, 8, 5.5, 3, ... ?

Question 3 options:

an=18+2.5n

an=18−2.5n

an=15.5−2.5n

an=15.5+2.5n
Question 4 (1 point)
Reggie has 195 trading cards in the first week. Each week, he purchases 16 more trading cards.

How many trading cards will he have in the 12th week?

Question 4 options:

387


371


-77


77

Question 5 (1 point)
What is the recursive rule for an=4n−1?

Question 5 options:

a1=3; an=an−1+4

a1=4; an=an−1−1

a1=3; an=an−1−1

a1=−1; an=an−1+4

Answer 1

Question 1) Option 1

Question 2) Option 1

Question 3) Option 3

Question 4) Option 1

Question 5) Option 1

Explanation:

Question 1) To calculate the common difference d of any sequence we subtract
`a_(n-1)` from
`a_(n)` for example
`a_(2)-a_(1)`=(-4) - (-15) = -4+15 = 11. Therefore option 1. (11) is the correct option for the sequence.

Question 2) If a sequence is
`a_(n) = 25- 3n`

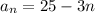
Then the 8th term of the sequence will be
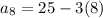`a_(8)= 25 - 3(8)` = 25-24 = 1. So option 1 is correct.

Question 3) Explicit rule for any arithmetic sequence is
`a_(n)= a_(1) + (common difference)(n)`

`a_(n)= 15.5 + (13-15.5)n`

`a_(n) = 15.5 -2.5n`

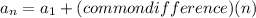
Therefore option 3 is correct.

Question 4) Reggie has 195 cards in first week and 16 cards are added every week.

So from this question
`a_(1) = 195` and common difference of the sequence is 16.

The sequence will be
`a_(n)= 195 + nd = (195 + 16n)`

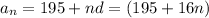
After 12th week number of cards will be

`a_(12)= 195 + (12)(16) = 195 + 192 =387`

So option 1 is correct.

Question 5) If the sequence is
`a_(n) = 4n-1`

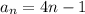
Then
`a_(1) = 4(1)-1 =(4-1) =3`

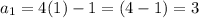
and
`a_(2) = 8-1 = 7`

Common difference will be 7-3 =4

Therefore
`a_(n)= a_(n-1)+4`

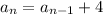
Option 1. is the correct answer.