Answer:
-8m
Explanation:
This question only requires to to substitute t = 0 and t = 1 into the equation to find the displacement.
Lets find the displacement at t = 0.

Lets find the displacement at t = 1.
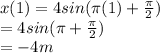
Total displacement = Final Position - Initial Position
= x(1)-x(0)
= -4m - 4m
= -8m