The displacement of a body is the distance that exists between the starting point and the end point of the trajectory of an object.
It is represented by a vector and does not depend on the path made by the object, but on the final and initial point.
To calculate this vector 'd' we do the following procedure.
Let
 and
and
 be the initial and final points of the trajectory of a body, so, the vector d is:
be the initial and final points of the trajectory of a body, so, the vector d is:
![d = [x_2-x_1]i + [y_2-y_1]j](https://img.qammunity.org/2020/formulas/physics/high-school/t0fbecwhjcnhwtexp3uhjsxfui20ogakfz.png)
For the given problem we are told that the object starts the movement from the origin, which is the point (0,0) and ends at the point (0, -8)
Then the vector is:
![d = [0 - 0]i + [-8 - 0]j\ m](https://img.qammunity.org/2020/formulas/physics/high-school/94l5t7i1sh5il6tbefvn8mifpyys4ei4dz.png)
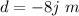
Then the displacement has a magnitude of 8 meters