Answer:
x can be cancelled
Explanation:
we are given
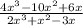
Firstly, we will factor numerator and denominator
and then we can factor it
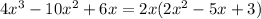
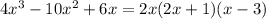
now, we can factor denominator
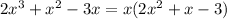
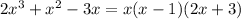
now, we can replace it
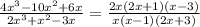
we can see that
both terms are having x common
so, x can be cancelled
So,
x can be cancelled