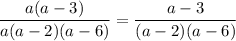Question

Simplify a^2-3a/a^3-8a^2+12a to lowest terms

Answer 1

In order to simplify a fraction, we have to find a common factor in both numerator and denominator. So, let's start by factor the expressions completely: at the numerator we have

`a^2-3a = a(a-3)`

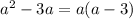
At the denominator we have

`a^3-8a^2+12a = a(a^2-8a+12) = a(a-2)(a-6)`

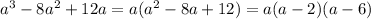
So, the fraction can be written as

`(a(a-3))/(a(a-2)(a-6))`

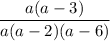
You can see that there is a factor
`a` in common, that can be simplified:

`(a(a-3))/(a(a-2)(a-6)) = (a-3)/((a-2)(a-6))`