Question

Two triangles are shown. The first triangle has sides x, 6 cm, and 12 cm, and the second triangle has corresponding sides 20 cm, 8 cm, and 16 cm. The two triangles above are similar. Find x using the ratio of the sides 12 cm and 16 cm: x 20 = 12 16 . Show your work. Find x using the ratio of the sides 6 cm and 8 cm. Show your work. Explain why the answers to (a) and (b) should be the same.

Answer 1

Given the two triangles are shown:

First triangle has sides x cm , 6 cm and 12 cm.

and

Second triangle has sides 20 cm , 8 cm and 16 cm.

Since, the given two triangles are Similar.

⇒there corresponding sides are in proportion.

i,e

`(x)/(20)=(6)/(8)=(12)/(16)`

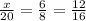
(a)

`(x)/(20)=(12)/(16)`

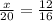
Solve for x;

By cross multiply we have;

`16x = 240`

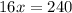
Divide both sides by 16 we get;

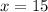`x = 15` cm

(b)

Find x using the ratio sides:

`(6)/(8) = (x)/(20)`

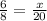
By cross multiply we have;

`120 = 8x`

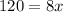
Divide both sides by 8 we get;

`15 = x`

or

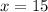`x = 15` cm

The value of x =15 cm in both a and b is same because the given two triangles are similar,

by definition of similarity, the given triangles have their corresponding sides are in proportion.