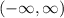Answer:
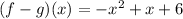
Domain:
Explanation:
we are given
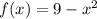
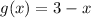
Calculation of (f-g)(x):
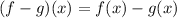
we can plug it
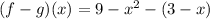
now, we can simplify it
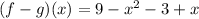
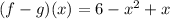
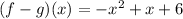
Domain:
we know that
domain is all possible values of x for which any function is defined
and f(x),g(x) and (f-g)(x) are polynomials
so, domain will be all real numbers
so, we get