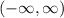Question

Let f(x)=9-x^2, g(x)=3-x. Find (f-g)(x) and its domain

Answer 1

`(f-g)(x)=-x^2+x+6`

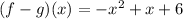
Domain:

`(-\infty,\infty)`

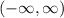
Explanation:

we are given

`f(x)=9-x^2`

`g(x)=3-x`

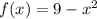
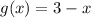
Calculation of (f-g)(x):

`(f-g)(x)=f(x)-g(x)`

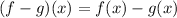
we can plug it

`(f-g)(x)=9-x^2-(3-x)`

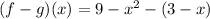
now, we can simplify it

`(f-g)(x)=9-x^2-3+x`

`(f-g)(x)=6-x^2+x`

`(f-g)(x)=-x^2+x+6`

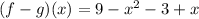
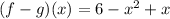
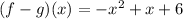
Domain:

we know that

domain is all possible values of x for which any function is defined

and f(x),g(x) and (f-g)(x) are polynomials

so, domain will be all real numbers

so, we get

`(-\infty,\infty)`