Question

Two cars leave an intersection at the same time, one heading east and the other heading south. Some time later the cars were 200 mi apart. If the car heading south travels 50 miles farther than the car going east, how far does the car heading east travel? Round the answer to the nearest tenth.

Answer 1

The car heading East travels 114 miles.

Explanation:

The distance traveled by the car heading East and the distance traveled by they car heading South and the distance between the cars form a right angled triangle with right angle at the starting point.

Using Pythogoras theorem,

`200^(2) =x^(2) +(x+50)^(2)`

`x^(2) +x^(2) +100x+2500=40000`

`2x^(2) +100x-37500=0`

`x^(2) +50x-18750=0`

`x=(-50+√(2500+4(18750)) )/(2)` or

`x=(-50-√(2500+4(18750)) )/(2)`

`x=(-50+278)/(2)` or
`x=(-50-278)/(2)`

x = 114 or x = -164

Ignoring the negative answer,

x = 114

Hence, the car heading East travels 114 miles.

Answer 2

114.2 miles

Explanation:

Let x miles be the distance traveled by car heading to east.

We have been given that one car is heading east and the other is heading south. Some time later the cars were 200 mi apart.

The car heading south travels 50 miles farther than the car going east, so the distance covered by car heading to south will be x+50 miles.

We can see from our given diagram that car heading to east and south form a right triangle with the intersection, so we will use Pythagoras theorem to find the distance (x) covered by car heading to east.

`x^2+(x+50)^2=200^2`

`x^2+x^2+100x+2500=40,000`

`2x^2+100x+2500-40,000=0`

`2x^2+100x-37,500=0`

`x^2+50x-18,750=0`

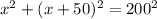
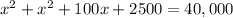
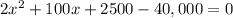
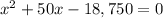
We will use quadratic formula to solve for x.

`x=(-b\pm√(b^2-4ac))/(2a)`

`x=(-50\pm√(50^2-4*1*-18,750))/(2*1)`

`x=(-50\pm√(2,500+75000))/(2)`

`x=(-50\pm√(77500))/(2)`

`x=(-50\pm 278.388218)/(2)`

`x=-164.1941\text{ or }x=114.1941`

`x\approx -164.2\text{ or }x\approx 114.2`

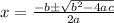
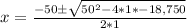
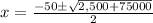
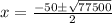
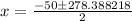
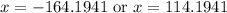
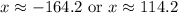
Since distance traveled by a car can not be negative, therefore, the car heading to east traveled 114.2 miles.