Question

The number of loops in the primary coil divided by the number of loops in the secondary coil equals the voltage in the primary coil divided by the voltage in the secondary coil if the volunteer attached to the primary coil read 100 volts what would the voltmeter attached to the secondary coil read

Answer 1

Answer :
`V_(s) = 100*(N_(p))/(N_(s))`

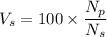
Explanation :

Given that, number of loop in the primary coil =
`N_(p)`

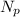
Number of loop in the secondary coil =
`N_(s)`

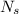
Voltage in primary coil = 100 Volt

Voltage in secondary coil =
`V_(s)`

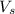
We know that

[tex]\dfrac{N_{p}}{N_{s}} = \dfrac{V_{s}}{V_{p}}[/tex]

`V_(s) = 100*(N_(p))/(N_(s))\ volt`

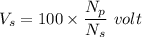
So, this is the required solution.