Answer:
The speed of the boat in still water is 13 miles/hour.
The speed of the current is 6 miles/hour.
Explanation:
Let the speed of the boat in still water be x
And speed of the current be y
When Irena's travelling downstream, the speed of the boat is:
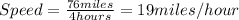
Traveling down stream the speed of the boat will be :
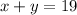 ..(1)
..(1)
When Irena's travelling upstream, the speed of the boat is:
Time taken by boat = 5 hours and 30 min = 5.5 hours (1 hour = 60 min)

Traveling down stream the peed of the boat will be :
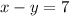 ..(2)
..(2)
On Solving both equation (1)and (2).
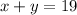
 putting value of x in (2) equation
putting value of x in (2) equation
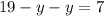
y = 6 miles/hour
Putting value of y in (1) equation:
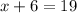 , x = 13 miles/hour
, x = 13 miles/hour
The speed of the boat in still water is 13 miles/hour.
The speed of the current is 6 miles/hour.