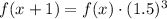Question

A certain culture of yeast increases by 50% every three hours. A scientist places 9 grams of the yeast in a culture dish. Write the explicit and recursive formulas for the geometric sequence formed by the growth of the yeast

Answer 1

The Explicit formula is
`f(x)=9(1.5)^(3x)`

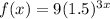
The recursive formula is

`f(x+1)=f(x)\cdot (1.5)^3`

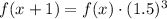
Explanation:

Given : A certain culture of yeast increases by 50% every three hours. A scientist places 9 grams of the yeast in a culture dish.

To find : Write the explicit and recursive formulas for the geometric sequence formed by the growth of the yeast?

Solution :

Number of grams of yeast in a culture dish initially a= 9 grams

A certain culture of year increases by 50 % every three hours.

r=50% , t=3

So, the explicit formula will be

`f(x)=a(1+(r)/(100))^x`

`f(x)=9(1+(50)/(100))^(3x)`

`f(x)=9(1+0.5)^(3x)`

`f(x)=9(1.5)^(3x)`

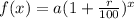
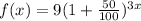
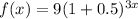
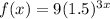
The recursive formula is

`f(x+1)=a(1+(r)/(100))^(x+1)`

`f(x+1)=9(1+(50)/(100))^(3(x+1))`

`f(x+1)=9(1+0.5)^(3x+3)`

`f(x+1)=9(1.5)^(3x+3)`

`f(x+1)=9(1.5)^(3x)\cdot (1.5)^3`

`f(x+1)=f(x)\cdot (1.5)^3`

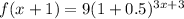
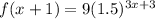
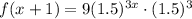
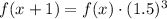
Therefore,

The Explicit formula is
`f(x)=9(1.5)^(3x)`

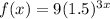
The recursive formula is

`f(x+1)=f(x)\cdot (1.5)^3`

Answer 2

Explicit:
`\bols{a_n=9(0.5)^(n-1)}`

Recursive:
`\bold{a_n=0.5(a_(n-1)),\quad a_1=9}`

Explanation:

A certain culture of yeast increases by 50% every three hours

⇒ rate (r) is
`(1.5)/(3)=0.5`

A scientist places 9 grams of the yeast in a culture dish.

⇒ first term of the sequence (a₁) = 9

The explicit rule for a geometric sequence is:
`a_n=a_1(r)^(n-1)`

⇒
`a_n=9(0.5)^(n-1)`

The recursive rule for a geometric sequence is:
`a_n=r(a_(n-1))`

⇒
`a_n=0.5(a_(n-1)),\quad a_1=9`