How high up a vertical wall will a 30-foot ladder reach if the foot of the ladder is placed 6 feet from the wall

Question

asked Sep 11, 2020 170k views

1 Answer

Ahmet DAL · Answer 1 · 2020-09-15T03:47:45+0000

Answer:

The height of wall where 30-foot ladder reaches is 29.39 foot.

Explanation:

Consider a triangle ABC showing AC be the 30 foot ladder that is resting on a wall AB and foot of ladder is 6 foot from the wall that is BC = 6

We have to find the height of wall where ladder is reaching.

Since building and foot of ladder makes a right angle at B.

Let AB be x foot.

PYTHAGORAS THEOREM STATES THAT THE SUM OF SQUARE OF BASE AND PERPENDICULAR IS EQUAL TO THE THE SQUARE OF HYPOTENUSE.

Applying Pythagoras theorem,

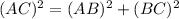
(AC)^2=(AB)^2+(BC)^2

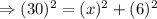
$\Rightarrow (30)^2=(x)^2+(6)^2$

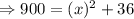
$\Rightarrow 900=(x)^2+36$

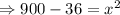
$\Rightarrow 900-36=x^2$

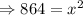
$\Rightarrow 864=x^2$

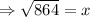
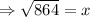
$\Rightarrow √(864)=x$

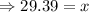
$\Rightarrow 29.39=x$

Thus, the height of wall where 30-foot ladder reaches is 29.39 foot.