The slope-intercept form of an equation of a line:
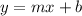
m - slope
b - y-intercept
We have the equations in the standard form. Convert to the slope-intercept form:
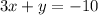 subtract 3x from both sides
subtract 3x from both sides
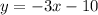
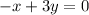 add x to both sides
add x to both sides
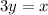 divide both sides by 3
divide both sides by 3
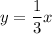
-----------------------------------------------------
We need only two points to plot a graph of each function.
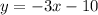
for x = 0 and for x = -3:
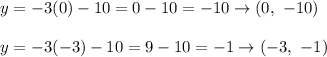
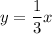
for x = 0 and for x = -3:
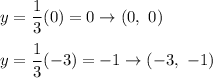
Look at the picture.