Answer:
(-11.385, -0.615)
Explanation:
Inequation: x^2+12x+7<0
Equation: x^2+12x+7=0
Use the quadratic formula to get the roots of the equation.

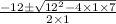
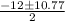
Root 1:
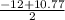
-0.615
Root 2:

-11.385
Then, the inequality can be expressed as
(x + 0.615)*(x + 11.385)<0
There are 2 ways to satisfy it:
x + 0.615 < 0 and x + 11.385 > 0
or
x + 0.615 > 0 and x + 11.385 < 0
For the first case:
x + 0.615 < 0 and x + 11.385 > 0
x < -0.615 and x > -11.385
In interval notation (-11.385, -0.615)
For the second case:
x + 0.615 > 0 and x + 11.385 < 0
x > -0.615 and x < -11.385
Which is impossible to satisfy. Therefore, the solution is (-11.385, -0.615)