Answer:
4 minutes.
Explanation:
We have been given that Jim ran four-fifths of a mile and dropped out of the 1600 meter race. His pace was 12 miles an hour until the point he dropped out of the race.
We will use formula
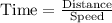 to solve our given problem.
to solve our given problem.
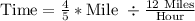
Since we know that dividing a fraction by another fraction is same as multiplying the 1st fraction by the reciprocal of the 2nd fraction.
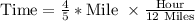
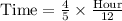
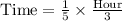
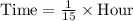
Let us convert our answer into minutes.
1 hour = 60 minutes.
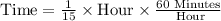
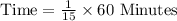
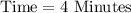
Therefore, Jim ran for 4 minutes.