Question

find the coordinates of point Z that splits the segment XY located 3/7 of the way between X(-2,1) and Y(4,5)

Answer 1

Z(-0.2, 2.2).

Step-by-step explanation:

We will use section formula when a point, say P, divides any segment ,say AB, internally in the ratio m:n.

`[x=(mx_2+nx_1)/(m+n), y= (my_2+ny_1)/(m+n)]`

We have been given the points of segment XY as X at (-2,1) and Y at (4,5) and ratio is 3:7.

`(x_1, y_1)=(-2,1)`

`(x_2, y_2)=(4,5)`

`m:n=3:7`

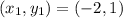
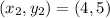
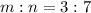
Upon substituting coordinates of our given points in section formula we will get,

`[x=((3*4)+(7*-2))/(3+7), y= (3*5+7*1)/(3+7)]`

`[x=(12-14)/(10), y= (15+7)/(10)]`

`[x=(-2)/(10), y= (22)/(10)]`

`[x=-0.2, y= 2.2]`

Therefore, coordinates of point Z will be (-0.2, 2.2).