Question

Question 17

The driver of a car traveling along a straight road with a
speed of 72KM ph observes a signboard which give the
speed limit to be 54KM ph. The signboard is 70m ahead
when the driver applies the brakes, calculate the
acceleration of the car which will cause the car to pass the
signboard at the stated speed limit?

Answer 1

So, the acceleration of the car is -1.25 m/s². In other word, the car is also decelerating by 1.25 m/s².

Introduction

Hi ! I will help you to discuss about "deceleration in a straight line movement". Please note in advance that deceleration is acceleration which has a negative value. When an object decelerates, the object will continue to move until it reaches a certain speed (which is less than before) or until it stops. The higher the deceleration value, an object that is moving will stop faster and cover a shorter distance.

Formula Used

In this opportunity, I will give you the following equation to express the relationship between final velocity and initial velocity, acceleration, and distance.

`\boxed{\sf{\bold{(v_t)^2= (v_0)^2 + 2 * a * s}}}`

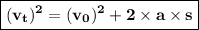
With the following condition:

• 
  `\sf{v_t}` = final velocity of an object (m/s)
• 
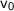  `\sf{v_0}` = initial velocity of an object (m/s)
• a = acceleration that happen (m/s²)
• s = the shift or distance of the object (m)

Problem Solving

We know that:

• 
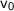  `\sf{v_0}` = initial velocity of an object = 72 km/h = 20 m/s
• 
  `\sf{v_t}` = final velocity of an object = 54 km/h = 15 m/s
• s = the shift or distance of the object = 70 m

Note :

• 1 m/s = 3.6 km/h. So 10 m/s = 36 km/h

What was asked ?

• a = acceleration that happen = ... m/s²

Step by step :

`\sf{(v_t)^2 = (v_0)^2 + 2 * a * s}`

`\sf{15^2 = 20^2 + 2 * a * 70}`

`\sf{225 = 400 + 140 * a}`

`\sf{140 a = -175}`

`\sf{a = (-175)/(140)}`

`\boxed{\sf{\bold{a = -1.25 \: m/s^2}}}`

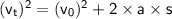
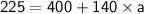
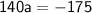
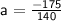
Conclusion

Here, we see that the acceleration is -1.25 m/s². In other words, the car is also decelerating by 1.25 m/s².