Question

Two containers are being filled with water. One begins with 8 gallons of water and is filled at a rate of 3.5 gallons per minute. The other begins with 24 gallons and is filled at 3.25 gallons per minute.

Part A: Write an equation that represents the amount of water w, in gallons, with respect to time t, in minutes, for each container.

Part B: Solve the system of equations. Show your work.

Part C: How long would it take for both of the containers to have the same amount of water? How much water would be in each container?

Answer 1

PART A:

w-3.5 t=8

w-3.25t=24

PART B:

t=64

and w= 232

PART C:

It will take 64 minutes for both of the containers to have the same amount of water.

The amount of water in each container is:

232 gallons.

Explanation:

PART A:

Let the water is filling in 't' minutes.

and 'w' denotes the amount of water in the container.

for container 1:

One begins with 8 gallons of water and is filled at a rate of 3.5 gallons per minute.

The equation is given by:

`w=8+3.5 t`

or
`w-3.5 t=8---------(1)`

for container 2:

The other begins with 24 gallons and is filled at 3.25 gallons per minute.

The equation is given by:

`w=24+3.25t`

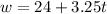
or
`w-3.25t=24--------(2)`

PART B:

on solving equation (1) and equation (2) by method of elimination we get:

subtract equation (2) by equation (1) to obtain:

`-3.5t+3.25t=8-24\\\\-0.25t=-16\\\\t=(16)/(0.25)\\\\t=64`

t=64

and putting the value of t in equation (1) to obtain:

`w-3.5* 64=8\\\\w-224=8\\\\w=232`

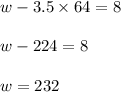
w= 232

PART C:

Hence it will take 64 minutes for both of the containers to have the same amount of water.

The amount of water in each container is:

232 gallons.