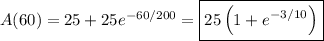Your answers for (a) and (c) are correct.
(b) Salt flows into the tank at a rate of
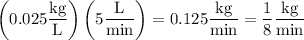
If
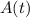 is the amount of salt (in kg) in the tank at time
is the amount of salt (in kg) in the tank at time
 (in min), then the salt flows out of the tank at a rate of
(in min), then the salt flows out of the tank at a rate of
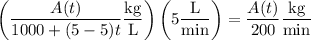
The net rate of change in the amount of salt in the tank at any time is then governed by the linear differential equation
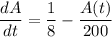
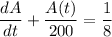
I'll solve this with the integrating factor method. The I.F. is

Distributing
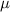 on both sides of the ODE gives
on both sides of the ODE gives
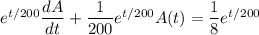
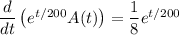
Integrate both sides.
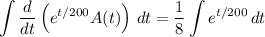
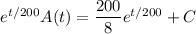
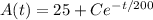
Given that
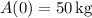 , we find
, we find
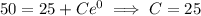
so that

Then the amount of salt in the tank after 1 hr = 60 min is