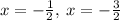Answer:
(a)
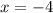
(b)
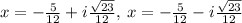
(c)
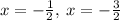
Explanation:
(a)
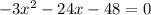
we can compare it with standard quadratic equation
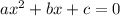
we can find a, b and c
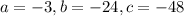
now, we can use quadratic formula
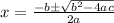
we can plug values
and we get
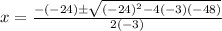
and we get
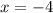
(b)
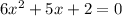
we can compare it with standard quadratic equation
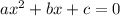
we can find a, b and c
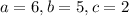
now, we can use quadratic formula
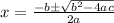
we can plug values
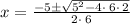
we get
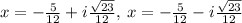
(c)
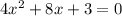
we can compare it with standard quadratic equation
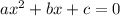
we can find a, b and c
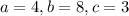
now, we can use quadratic formula
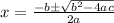
we can plug values
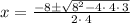
we get