Answer:
The graph in the attached figure
Explanation:
we have
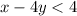 ----> inequality A
----> inequality A
solve for y
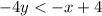
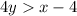
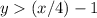
The solution of the inequality A is the shaded area above the dashed line
The slope of the dashed line is positive
The y-intercept is the point

The x-intercept is the point
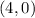
 ----> inequality B
----> inequality B
The solution of the inequality B is the shaded area below the dashed line
The slope of the dashed line is positive
The y-intercept is the point

The x-intercept is the point
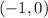
Using a graphing tool
The solution of the system of inequalities in the attached figure