If a, b and c are a Pythagorean triple, then:
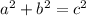
for a ≤ b < c.
We have:
A) 11, 60, 61
check:
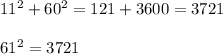
CORRECT
B) 6, 8, 15
These are not the sides of the triangle because 6 + 8 = 14 < 15
C) 5, 11, 12
check
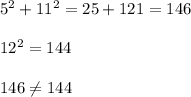
INCORRECT
D) 9, 24, 25
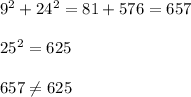
INCORRECT
Answer: A) 11, 60, 61
2)
If a, b, c are the sides of the triangle, then:
a + b > c and a + c > b and b + c > a.
We have 14, 48, x. Therefore:
x < 14 + 48
x < 62
and
x + 14 > 48
x > 34
therefore 34 < x < 62
If 34 < x < 48, then:
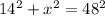
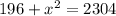 subtract 196 from both sides
subtract 196 from both sides
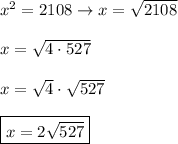
If 48 < x < 62, then:
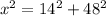
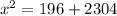
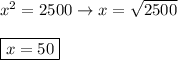
Answer: D) 50