Question

What is the value of sinθ given that (3, −7) is a point on the terminal side of θ ? −758√58 758√58 358√58 −358√58?

Answer 1

`-(7√(58))/(58)`

Explanation:

Answer 2

`\boxed{\sin(\theta)=-(7)/(58)√(58)}`

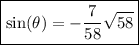
Step-by-step explanation

The given point
`(3,-7)` tells us that the terminal side of
`\theta` is in the fourth quadrant.

From the diagram in the attachment,

We can use the Pythagoras Theorem to find the length of the hypotenuse of the right triangle.

Let the hypotenuse be
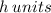`h\: units`. Then,

`h^2=7^2+3^2`

`h^2=49+9`

`h^2=58`

`\Rightarrow h=√(58)`

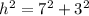
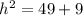
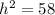
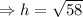
Now we use the sine ratio;

`\sin(\theta)=(Opposite)/(Hypotenuse)`.

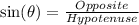But since the terminal side of
`\theta` is in the fourth quadrant, the sine ratio must be negative.

This implies that;

`\sin(\theta)=-(7)/(√(58))`.

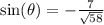We rationalize the denominator to get;

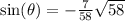`\sin(\theta)=-(7)/(58)√(58)`.