Take any two pairs of the given points and make vectors out of them. For example, the vector from A to B is
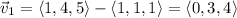
and the vector from A to C is
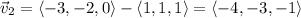
These vectors lie in the same plane (the one we want). We can get a third vector that is normal to the plane by taking their cross product (details omitted).
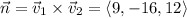
If
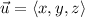 is an arbitrary vector, then the vector from any of the points A, B, or C to
is an arbitrary vector, then the vector from any of the points A, B, or C to
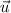 will lie in our plane. That is, if we start from A,
will lie in our plane. That is, if we start from A,
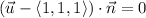
and this reduces to the equation of the plane,
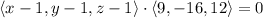

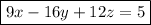
This follows immediately from the cross product identity
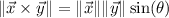
where
 is the angle between
is the angle between
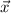 and
and
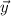 . The left side corresponds to the area of the parallelogram spanned by
. The left side corresponds to the area of the parallelogram spanned by
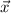 and
and
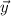 ; half of this area would be that of a triangle. (see attached)
; half of this area would be that of a triangle. (see attached)
In our case, we have
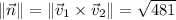
so the area of ABC is
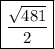 .
.
- Angle between A to B and between C to B
We already know the first vector,
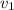 .
.
The vector from C to B is
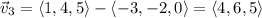
Recall the dot product identity,
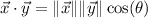
Then
