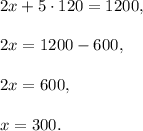Question

Travis has $60 in dimes and quarters.If he could switch the numbers of dimes with the number of quarter, he would have $87. How many of each coin does Travis

Answer 1

300 dimes and 120 quarters

Explanation:

Let x be the number of dimes and y be the number of quarters Travis has. Travis has $60 (6000 cents) in dimes and quarters, then

`10x+25y=6000.`

If he could switch the numbers of dimes with the number of quarter, he would have y dimes and x quarters. In total this amount of money is $87 (8700 cents), then

`10y+25x=8700.`

Solve the system of two equations:

`\left\{\begin{array}{l}10x+25y=6000\\ \\10y+25x=8700\end{array}\right.\Rightarrow \left\{\begin{array}{l}2x+5y=1200\\ \\2y+5x=1740\end{array}\right..`

Multiply the 1st equation by 5, the 2nd equation by 2 and subtract them:

`\left\{\begin{array}{l}10x+25y=6000\\ \\10x+4y=3480\end{array}\right.\Rightarrow 21y=2520,\ y=120.`

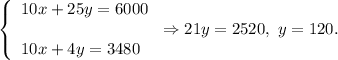
Then

`2x+5\cdot 120=1200,\\ \\2x=1200-600,\\ \\2x=600,\\ \\x=300.`