Answer: The number of excess electrons that the drop contains are 3.
Step-by-step explanation:
We are given:
Charge on millikan's oil drops =
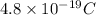
To calculate the number of excess electrons, we divide the charge on millikan's oil drop by the change on 1 electron.
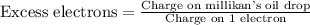
We know that:
Charge on 1 electron =
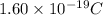
Putting values in above equation, we get:
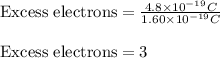
Hence, the number of excess electrons that the drop contains are 3.