Question

Which system of inequalities is represented on this graph?

Answer 1

It is the second answer choice

Explanation:

Answer 2

The correct option is 2.

Explanation:

If a line passes through two points
`(x_1,y_1)` and
`(x_2,y_2)`, then the equation of line is

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

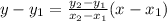
From the given graph it is clear that the solid line passes through the points (0,2) and (1,0). So, the related equation of solid line is

`y-2=(0-2)/(1-0)(x-0)`

`y-2=-2x`

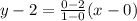
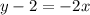
Add 2 on both sides.

`y=-2x+2`

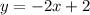
The sign of inequality must be ≤ because the points on the line are included in the solution set and the shaded region is below the line.

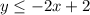`y\leq -2x+2` .... (1)

From the given graph it is clear that the solid line passes through the points (0,-1) and (1,0). So, the related equation of solid line is

`y-(-1)=(0-(-1))/(1-0)(x-0)`

`y+1=x`

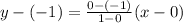
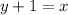
Subtract 1 from both sides.

`y=x-1`

The sign of inequality must be < because the points on the line are not included in the solution set and the shaded region is below the line.

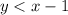`y<x-1` .... (2)

The system of inequalities is

`y\leq -2x+2`

`y<x-1`

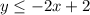
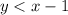
Therefore, the correct option is 2.