Question

Two chords intersect inside a circle. the lengths of the segment of one chord are 4 and 6. the lengths of the segments of the other chord are 3 and _

7
8
9

Answer 1

Answer: The lengths of the segments of the other chord are 3 units and 8 units.

Step-by-step explanation: As shown in the attached figure below, let the chords AB and CD intersect inside the circle at the point O, where

AO = 4 units, OB = 6 units, Co = 3 units.

We are to find the length of OD.

We have the following theorem :

Intersecting Chord Theorem: When two chords intersect each other inside a circle, then the products of their segments are equal.

Applying the above theorem in the given circle, we must have

`AO* OB=CO* OD\\\\\Rightarrow 4*6=3* OD\\\\\Rightarrow 24=3OD\\\\\Rightarrow OD=(24)/(3)\\\\\Rightarrow OD=8.`

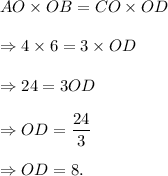
Thus, the lengths of the segments of the other chord are 3 units and 8 units.

Answer 2

8

Explanation:

The product of the segment lengths of one chord is equal to the product of the segment lengths of the other chord:

4 · 6 = 3 · 8