Answer:The correct answer is option A.
Step-by-step explanation:
We have been given that
Probability that the land has oil =
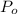 = 45% = 0.45
= 45% = 0.45
Accuracy rate of the kit indicating the oil in the soil =
 = 80 %= 0.80
= 80 %= 0.80
Rate of the kit indicating no oil in the soil =
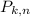 1 - 0.8 = 0.2
1 - 0.8 = 0.2
Probability of the land has oil and test kit predicts that there is no oil:(And means multiplication, so we will multiply the above two probabilities)
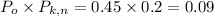
Hence, the probability that the land has oil and the test predicts that there is no oil is 0.09.