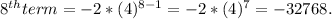Question

determine if the sequence is geometric if it is find the common ratio the 8th term and the explicit formula can someone check my work

Answer 1

You can check the answer by yourself after seeing the below answer.

Explanation:

A sequence is geometric only if has common ratio i.e.
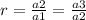`r=(a2)/(a1) =(a3)/(a2)` whiere a1,a2 and a3 are first,second and third term of the sequence respectively.

1) Common ratio
`r=(-18)/(-3)=(-108)/(-18)=6\\`

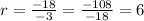
Explicit formula
`a_(n) =a_(1) .r^(n-1)`

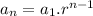
Now using the above formula, we can find
`8^(th) term=-3*(6)^(8-1) =-3*6^(7)=-839808.`

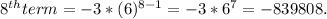
2) Here

`(a2)/(a1)\\eq (a3)/(a2)\\(-2)/(-4)\\eq (1)/(-2)\\(1)/(2)\\eq(1)/(-2)` so this is not geometric sequence so no need to proceed further.

3) Common ratio
`r=(15)/(-3)=(-75)/(15)=-5\\`

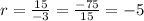
Explicit formula
`a_(n) =a_(1) .(-5)^(n-1)`

Now using the above formula, we can find
`8^(th) term=-3*(-5)^(8-1) =-3*(-5)^(7)=234375.`

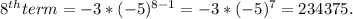
4) Common ratio
`r=(-6)/(1)=(36)/(-6)=-6\\`

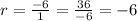
Explicit formula
`a_(n) =a_(1) .(-6)^(n-1)`

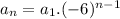
Now using the above formula, we can find
`8^(th) term=1*(-6)^(8-1) =1*(-6)^(7)=-279936.`

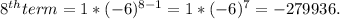
5)Common ratio
`r=(-8)/(4)=(16)/(-8)=-2\\`

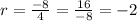
Explicit formula
`a_(n) =a_(1) .(-2)^(n-1)`

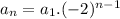
Now using the above formula, we can find
`8^(th) term=4*(-2)^(8-1) =4*(-2)^(7)=-512.`

6)Common ratio
`r=(-8)/(-2)=(-32)/(-8)=4\\`

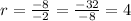
Explicit formula
`a_(n) =a_(1) .(4)^(n-1)`

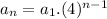
Now using the above formula, we can find
`8^(th) term=-2*(4)^(8-1) =-2*(4)^(7)=-32768.`