Question

In the figure below, the segment is parallel to one side of the triangle. The ratio of 12 to y is 1:2 1:3 1:4 2:3

Answer 1

Option 2.

Explanation:

In the figure below, the segment is parallel to one side of the triangle.

Given: BC║DE

In triangle ABC and ADE,

`\angle BAC\cong \angle DAE` (Reflexive property)

`\angle ABC\cong \angle ADE` (Corresponding angles)

By AA property of similarity,

`\triangle ABC\sim \triangle ADE`

Corresponding parts of similar triangle are proportional.

`(DE)/(AB)=(AD)/(AB)`

`(12)/(y)=(15)/(15+30)`

`(12)/(y)=(15)/(45)`

`(12)/(y)=(1)/(3)`

The ratio of 12 to y is 1:3. Therefore, the correct option is 2.

Answer 2

Option B. 1 : 3

Explanation:

There are two triangles shown in the picture attached ΔABC and ΔCD.

In these triangles sides AB and DE are parallel and BC is transverse line so ∠ABC = ∠EDC (corresponding angles)

Similarly AC is transverse to parallel lines AB and DE, so ∠BAC = ∠DEC (corresponding angles)

∠ACB is common in both the triangles.

Therefore ΔABC and ΔDEC are similar.

We know in similar triangles corresponding sides are in the same ratio.

`(AB)/(ED)=(AC)/(EC)`

`(y)/(12)=(30+15)/(15)=(45)/(15)=3:1`

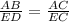
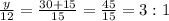
Therefore ratio of y and 12 is equal to 3 : 1

Or ratio of 12 to y is 1 : 3

Option B is the answer.