Question

Find the orthocenter of △ABC. A(2, 3), B(−4, −3), C(2, −3)

A. (2, −3)

B. (−1, 0)

C. (0, −1)

D. (−2, 1)

Answer 1

ANSWER


`\boxed { A. \: \: (2,-3) }`

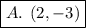
EXPLANATION.

The orthocenter is the point of intersection of any two altitudes of the triangle.

First, you need to determine the slope of each side of the triangle.

△ABC has vertices A(2, 3), B(−4, −3), C(2, −3).


`slope \: of \: AB = (3 - - 3)/(2 - - 4) = (6)/(6) = 1`


`slope \: of \: AC = ( 3 - - 3)/(2 - 2) = (6)/(0)`

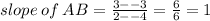
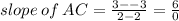
This line has undefined slope, which means it is a vertical line.


`slope \: of \: BC = ( - 3 - - 3)/( 2 - - 4) = (0)/(6) = 0`

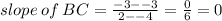
The slope of this line is zero, meaning the line is a horizontal line.

This implies that side BC and side AC of the given triangle are perpendicular and will intersect at C since they are the altitudes of triangle ABC.

Hence the orthocentre is


`(2,-3)`

See diagram in attachment.