Question

Jerome solved the equation below by graphing.

log_2x+log_2(x-2)=3

Which of the following shows the correct system of equations and solution?

a.) y_1=logx/log2 +log(x-2)/log2 y_2=3, x=3

b.) y_1=logx/log2 + log(x-2)/log2 y_2=3, x=4

c.) y_1=logx+log(x-2) y_2=3, x=33

d.) y_1=logx +log(x-2) y_2=3, x=44

Answer 1

Jerome rewrote the logarithms as

`\log_2x=(\log x)/(\log2)`

`\log_2(x-2)]=(\log(x-2))/(\log 2)`

which eliminates C and D.

Solve the equation:

`\log_2x+\log_2(x-2)=\log_2x(x-2)=3\implies 2^(\log_2x(x-2))=2^3\implies x(x-2)=8`

`\implies x^2-2x-8=(x-4)(x+2)=0\implies x=4\text{ or }x=-2`

`\log_b(-2)` is undefined for any base
`b` (where the logarithm is real-valued), so we omit that solution.

This makes B the answer.

Answer 2

Option b -
`y_1=(\log x)/(\log 2)+(\log (x-2))/(\log 2), y_2=3, x=4`

Explanation:

Given : Jerome solved the equation below by graphing.

`\log_2x+\log_2(x-2)=3`

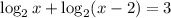
To find : Which of the following shows the correct system of equations and solution?

Solution :

Two system of equations formed from given equation,

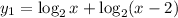
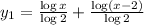`y_1=\log_2x+\log_2(x-2)`

`y_1=(\log x)/(\log 2)+(\log (x-2))/(\log 2)` ......[1]

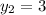`y_2=3` .........[2]

Now, we plot these two equations and the intersection of these two equation is the solution.

The intersection point is (4,3)

Therefore, The solution of given equation is x=3

Hence, Option b is correct.