Question

Pathagorem therom missing leg

Answer 1

Explanation:

Answer: You have to find the square root of 95

Explanation:

A^2+b^2=c^2

12^2-7^2= square root of 95

Answer 2

Hey there!

Most importantly, the pythagorean theorum is
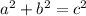`a^(2) + b^(2) = c^(2)`, where a and b are the two legs and c is the hypotenuse.

Let's do #3 first.

We're trying to find the missing leg in this equation.

The leg that is 7 inches will be our a, and the hypotenuse, which is c, is 12 inches. Let's plug those values into the equation so we can solve for b, the missing length of the other leg.

`7^(2) + b^(2) = 12^(2)`

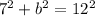
Square 7 and 12. You do that by multiplying it by itself.

`49 + b^(2) = 144`

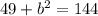
Subtract 49 from each side of the equation.

`b^(2) = 95`

Find square root of both sides.

b =
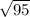`√(95)` or approximately 9.747

In radical form, the missing lenth of the leg is
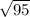`√(95)`, and rounded to the nearest thousandth it is 9.747 inches.

Now, let's do #6.

Both the values for a and b will be 18, since the length of both of the legs are 18.

`18^(2) + 18^(2) =c^(2)`

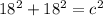
Square 18 in both places.

`324 + 324 = c^(2)`

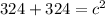
Add.

`648 = c^(2)`

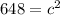
Find the square root of both sides.

c =
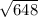`√(648)` or approximately 25.456

In radical form, the hypotenuse is [tex]\sqrt{648}, and rounded to the nearest thousandth it is 25.456.

Hope this helps!