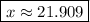(a) The differential equation
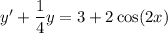
is linear, so we can use the integrating factor method. We have I.F.
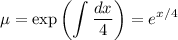
so that multiplying both sides by
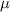 gives
gives
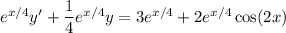
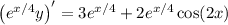
Integrate both sides. (Integrate by parts twice on the right side; I'll omit the details.)
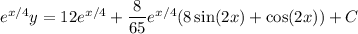
Solve for
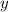 .
.
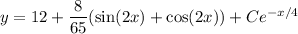
Given that
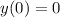 , we find
, we find
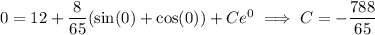
and the particular solution to the initial value problem is
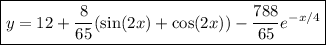
As
 gets large, the exponential term will converge to 0. We have
gets large, the exponential term will converge to 0. We have
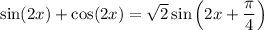
which means the trigonometric terms will oscillate between
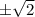 . So overall, the solution will oscillate between
. So overall, the solution will oscillate between
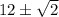 for large
for large
 .
.
(b) We want the smallest
 such that
such that
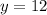 , i.e.
, i.e.
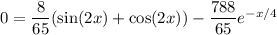
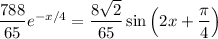
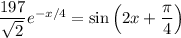
Using a calculator, the smallest solution seems to be around