Answer:
38.33 m
Explanation:
We are given that Mary is flying a kite with a 50 - meter string.
The string is making a 50 degrees angle with the ground
We have to find the height above the ground of the kite
Let x be the height of kite above the ground

Height of string =Hypotenuse
In aright angled triangle ABC

Substitute the values then we get
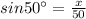
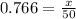
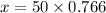

Hence, the height of kite above the ground=38.33 m